Determinanten Rechner

Die Determinante einer quadratischen Matrix $A=\left(a_{ij}\right)$ der Dimension n ist eine reelle Zahl, die linear von jedem Spaltenvektor der Matrix abhängt. Wir bemerken $\det \left(A\right)$ ou $\left|A\right|$ die Determinante der quadratischen Matrix A.

$\det \left(\begin{array}{c}{m}_{1;n}\dots \; <!--\; horizontal\; ellipsis\; -->m_{m_{i;n}}\\ ⋮\; <!--\; vertical\; ellipsis\; -->\ddots \; <!--\; down\; right\; diagonal\; ellipsis\; -->⋮\; <!--\; vertical\; ellipsis\; -->\\ m_{n;1}\dots \; <!--\; horizontal\; ellipsis\; -->m_{n;n}\end{array}\right)=\left|\begin{array}{c}{m}_{1;1}\dots \; <!--\; horizontal\; ellipsis\; -->m_{1;n}\\ ⋮\; <!--\; vertical\; ellipsis\; -->\ddots \; <!--\; down\; right\; diagonal\; ellipsis\; -->⋮\; <!--\; vertical\; ellipsis\; -->\\ m_{n;n}\dots \; <!--\; horizontal\; ellipsis\; -->m_{n;n}\end{array}\right|$

Die einfachste Formel zur Berechnung der Determinante ist die Leibeiniz-Formel:

Eigenschaften von Determinanten

• Die Determinante ist gleich 0, wenn,
  • Zwei Zeilen in der Matrix sind gleich.
  • La matrice a au moins une ligne ou colonne égale à zéro.
  • Die Matrix ist einzigartig.
• Das Subtrahieren der Zeile i von der Zeile j n ändert den Wert der Determinante nicht.

Determinante Berechnungsmethode

Wenn A eine nxn-Matrix ist, lautet die Formel: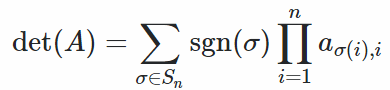

Beispiel

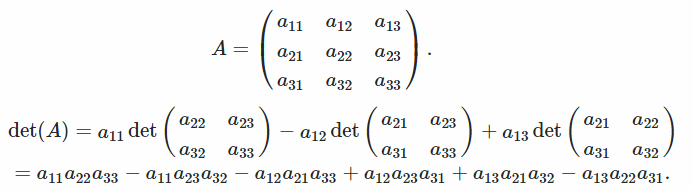
Diese Methode transformiert die Matrix in eine reduzierte Reihenebenenform, indem Zeilen oder Spalten ausgetauscht, zur Zeile hinzugefügt und mit einer anderen Zeile multipliziert werden, um maximal Nullen anzuzeigen.

Für jeden Pivot multiplizieren wir mit -1.