Matrix Determinant Calculator

Instantly compute the determinant of any square matrix and learn the theory behind it.

What is a Determinant?

The determinant of a square matrix $A=\left(a_{ij}\right)$ of dimension n is a real number which depends linearly on each column vector of the matrix. We denote by $\det \left(A\right)$ or $\left|A\right|$ the determinant of the square matrix A.

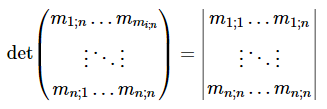
Properties of determinants

• The determinant is equal to 0 if,
  • Two lines in the matrix are equal.
  • The matrix has at least one row or column equal to zero.
  • The matrix is ​​unique.
• Subtracting row i from row j n times does not change the value of the determinant.
• If two rows or columns are swapped, the sign of the determinant changes from positive to negative or from negative to positive.
• The determinant of the identity matrix is equal to 1, $\det \left(I_n\right)=1$
• The determinants of A and its transpose are equal, $\det \left(A^T\right)=\det \left(A\right)$
• $\det \left(A^{-1}\right)=\frac{1}{\det \left(A\right)}={\left[\det \left(A\right)\right]}^{-1}$
• If A and B have matrices of the same dimension, $\det \left(AB\right)=\det \left(A\right)\times \det \left(B\right)$
• $\det \left(cA\right)=c^{n}x\det \left(A\right)$
• $\det \left(A\right)=a_n{a}_{22}\dots a_{nn}=\prod _{i=1}^n{a}_{ii}$ , if the matrix A is triangular $a_{ij}=0$ et $i\ne j$ , the determinant is equal to the product of the diagonal of the matrix.

Methods to Calculate a Determinant

Cofactor Expansion (Laplace)

Cofactor expansion is used for small matrices because it becomes inefficient for large matrices compared to the matrix decomposition methods.

The formula for calculating the expansion of Place is given by:

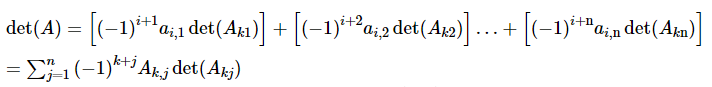
Where $k$ is a fixed choice of $i\in \{1,2,\dots ,n\}$ and $\det \left(A_{kj}\right)$ is the minor of element $a_{ij}$.

Example

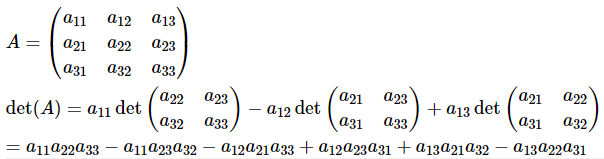
Leibniz Formula

Permutation-based formula (theoretical, less efficient)

Where $S_n\in \{1,2,\dots ,n\}$ is a set of permutations from 1 to n, and $\mathrm{sgn}$ is a function that defines the sign int the set ${\mathrm{S}}_n$, which returns +1 for even permutations and -1 for odd permutations.

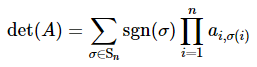
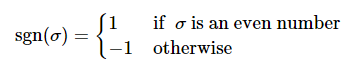
Example

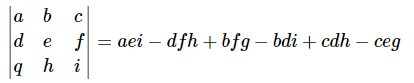
Gauss Elimination

Efficient for large matrices, row operations explained

Gauss elimination is also used to find the determinant by transforming the matrix into a reduced row echelon form by swapping rows or columns, add to row and multiply of another row in order to show a maximum of zeros.

For each pivot we multiply by -1.

Where $p$ is the number of the permutations and $A[k,j]$ is the pivot calculated in step j.

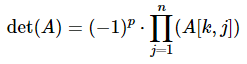
Rule of Sarrus

Quick trick for 3×3 matrices

The Sarrus Rule is used for computing only 3x3 matrix determinant. The method consists in adding the first two columns after the first three columns then calculating the product of the coefficients of each diagonal according to the following scheme:

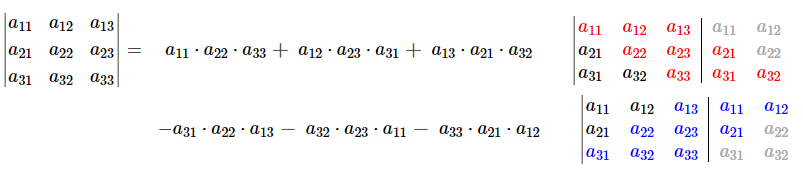
Bareiss algorithm(Montante's method)

The Bareiss algorithm calculates the echelon form of the matrix with integer values. It looks a bit like the Gaussian elimination algorithm and in terms of the number of operations performed. Divisions made have no remainder.

The determinant is determined after several reductions of the matrix to the last row by dividing on a pivot of the diagonal with the formula:

Step-by-Step Examples

### Example 1: Determinant of a 2×2 Matrix For a 2×2 matrix: \[ A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \] The determinant is computed as: \[ \det(A) = ad - bc \] **Example Calculation:** \[ A = \begin{bmatrix} 3 & 5 \\ 2 & 4 \end{bmatrix} \] \[ \det(A) = (3 \cdot 4) - (5 \cdot 2) = 12 - 10 = 2 \] --- ### Example 2: Determinant of a 3×3 Matrix (Rule of Sarrus) For a 3×3 matrix: \[ B = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \] The determinant is computed using Sarrus’ Rule: \[ \det(B) = (ae i + b f g + c d h) - (c e g + a f h + b d i) \] **Example Calculation:** \[ B = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} \] \[ \det(B) = (1\cdot5\cdot9 + 2\cdot6\cdot7 + 3\cdot4\cdot8) - (3\cdot5\cdot7 + 1\cdot6\cdot8 + 2\cdot4\cdot9) \] \[ = (45 + 84 + 96) - (105 + 48 + 72) \] \[ = 225 - 225 = 0 \] Since the rows are linearly dependent, the determinant is **0**. --- ### Example 3: Determinant of a 4×4 Matrix (Gaussian Elimination) Consider the 4×4 matrix: \[ C = \begin{bmatrix} 1 & 2 & 0 & 1 \\ 3 & 4 & 1 & 0 \\ 0 & 2 & 3 & 4 \\ 5 & 0 & 2 & 1 \end{bmatrix} \] We will reduce this to upper triangular form using Gaussian elimination. **Step 1: Eliminate below first pivot (1)** Subtract \(3 \cdot R_1\) from \(R_2\), and \(5 \cdot R_1\) from \(R_4\): \[ R_2 \to R_2 - 3R_1, \quad R_4 \to R_4 - 5R_1 \] \[ \begin{bmatrix} 1 & 2 & 0 & 1 \\ 0 & -2 & 1 & -3 \\ 0 & 2 & 3 & 4 \\ 0 & -10 & 2 & -4 \end{bmatrix} \] --- **Step 2: Eliminate below second pivot (-2)** Add \(R_2\) to \(R_3\) and \(5R_2\) to \(R_4\): \[ R_3 \to R_3 + R_2, \quad R_4 \to R_4 + 5R_2 \] \[ \begin{bmatrix} 1 & 2 & 0 & 1 \\ 0 & -2 & 1 & -3 \\ 0 & 0 & 4 & 1 \\ 0 & 0 & 7 & -19 \end{bmatrix} \] --- **Step 3: Eliminate below third pivot (4)** \[ R_4 \to R_4 - \frac{7}{4} R_3 \] \[ \begin{bmatrix} 1 & 2 & 0 & 1 \\ 0 & -2 & 1 & -3 \\ 0 & 0 & 4 & 1 \\ 0 & 0 & 0 & -\frac{83}{4} \end{bmatrix} \] --- **Step 4: Compute determinant as product of diagonal entries:** \[ \det(C) = 1 \cdot (-2) \cdot 4 \cdot \left(-\frac{83}{4}\right) = 1 \cdot (-2) \cdot 4 \cdot -\frac{83}{4} = 166 \] So, the determinant of \(C\) is **166**. ---

Key takeaways from examples

• 2×2 is straightforward: \( \det\! = ad - bc \).
• 3×3 can be solved quickly with Sarrus’ Rule.
• 4×4 or higher: Gaussian elimination is efficient and avoids tedious cofactor expansion.

Use the appropriate method depending on matrix size: direct formulas for small matrices, elimination or optimized algorithms for larger ones.

Frequently Asked Questions

What is the determinant of a matrix?

The determinant is a scalar value that can be computed from a square matrix. It provides important information about the matrix, including whether it's invertible (non-zero determinant) or singular (zero determinant). The determinant represents the scaling factor of the linear transformation described by the matrix and the signed volume of the parallelepiped formed by the matrix columns.

How do you calculate the determinant of a 2×2 matrix?

For a 2×2 matrix [[a, b], [c, d]], the determinant is calculated using the formula: det(A) = ad - bc. Simply multiply the main diagonal elements (a × d) and subtract the product of the anti-diagonal elements (b × c). For example, for matrix [[3, 2], [1, 4]], the determinant is (3×4) - (2×1) = 12 - 2 = 10.

What is the formula for a 3×3 matrix determinant?

For a 3×3 matrix, use the rule of Sarrus or cofactor expansion. Using cofactor expansion along the first row: det(A) = a(ei-fh) - b(di-fg) + c(dh-eg), where the matrix is [[a,b,c], [d,e,f], [g,h,i]]. Alternatively, you can use the rule of Sarrus by repeating the first two columns and calculating the sum of products along diagonals.

Can non-square matrices have determinants?

No, determinants are only defined for square matrices (n×n matrices where the number of rows equals the number of columns). Rectangular matrices like 2×3 or 4×2 do not have determinants. This is because the determinant represents properties of linear transformations that preserve dimension, which only square matrices can represent.

What does a zero determinant mean?

A zero determinant indicates that the matrix is singular (non-invertible). This means: 1) The matrix rows/columns are linearly dependent, 2) The matrix transformation collapses at least one dimension, 3) The system of equations represented by the matrix has either no solution or infinitely many solutions, 4) The matrix cannot be inverted, and 5) The transformation reduces the volume to zero.

What is the difference between minor and cofactor?

A minor M(i,j) is the determinant of the submatrix formed by deleting row i and column j from the original matrix. A cofactor C(i,j) is the minor multiplied by (-1)^(i+j), which applies a sign based on position. The cofactor includes the alternating sign pattern (checkerboard of + and - signs), while the minor is always positive. Cofactors are used in determinant calculation and finding matrix inverses.

How do you find the determinant of large matrices (4×4 and beyond)?

For matrices larger than 3×3, use methods like: 1) Cofactor expansion (Laplace expansion) - recursively expand along any row or column, 2) Row reduction to triangular form - the determinant equals the product of diagonal elements times (-1)^(number of row swaps), 3) LU decomposition - det(A) = det(L) × det(U), or 4) Use a determinant calculator for efficiency. Manual calculation becomes impractical for large matrices due to computational complexity.

What are the properties of determinants?

Key determinant properties include: 1) det(AB) = det(A) × det(B), 2) det(A^T) = det(A), 3) det(kA) = k^n × det(A) for n×n matrix, 4) Swapping two rows/columns changes the sign, 5) Adding a multiple of one row to another doesn't change the determinant, 6) If a row/column is all zeros, det = 0, 7) For triangular matrices, det = product of diagonal elements, 8) det(A^(-1)) = 1/det(A).

What is Cramer's Rule and how does it use determinants?

Cramer's Rule uses determinants to solve systems of linear equations Ax = b. For each variable x_i, the solution is x_i = det(A_i)/det(A), where A_i is matrix A with column i replaced by vector b. This method works only when det(A) ≠ 0. While elegant for small systems, it's computationally inefficient for large systems compared to methods like Gaussian elimination.

What is the geometric interpretation of a determinant?

Geometrically, the absolute value of a determinant represents the volume scaling factor of the linear transformation. For a 2×2 matrix, |det(A)| is the area of the parallelogram formed by column vectors. For a 3×3 matrix, it's the volume of the parallelepiped. The sign indicates orientation: positive preserves orientation (right-handed to right-handed), negative reverses it. A zero determinant means the transformation collapses the space to a lower dimension.

How do you calculate determinants using row reduction?

To find a determinant using row reduction: 1) Use elementary row operations to transform the matrix to upper triangular form, 2) Keep track of operations: row swaps change the sign, multiplying a row by k multiplies det by k, adding multiples of rows doesn't change det, 3) Once in triangular form, the determinant is the product of diagonal elements times any sign changes. This method is efficient for large matrices and is used by most calculators.

Why is the determinant important in linear algebra?

Determinants are crucial because they: 1) Determine if a matrix is invertible (det ≠ 0), 2) Calculate matrix inverses using adj(A)/det(A), 3) Solve linear systems via Cramer's rule, 4) Find eigenvalues (det(A - λI) = 0), 5) Measure volume changes in transformations, 6) Test linear independence of vectors, 7) Appear in calculus (Jacobian determinants), and 8) Are used in physics, engineering, and computer graphics for rotations and transformations.