Calcolatrice determinante di matrici

Il determinante di una matrice quadrata$A=\left(a_{ij}\right)$ di dimensione n è un numero reale che dipende linearmente da ogni vettore colonna della matrice. Notiamo$\det \left(A\right)$ ou $\left|A\right|$ il determinante della matrice quadrata A.

$\det \left(\begin{array}{c}{m}_{1;n}\dots \; <!--\; horizontal\; ellipsis\; -->m_{m_{i;n}}\\ ⋮\; <!--\; vertical\; ellipsis\; -->\ddots \; <!--\; down\; right\; diagonal\; ellipsis\; -->⋮\; <!--\; vertical\; ellipsis\; -->\\ m_{n;1}\dots \; <!--\; horizontal\; ellipsis\; -->m_{n;n}\end{array}\right)=\left|\begin{array}{c}{m}_{1;1}\dots \; <!--\; horizontal\; ellipsis\; -->m_{1;n}\\ ⋮\; <!--\; vertical\; ellipsis\; -->\ddots \; <!--\; down\; right\; diagonal\; ellipsis\; -->⋮\; <!--\; vertical\; ellipsis\; -->\\ m_{n;n}\dots \; <!--\; horizontal\; ellipsis\; -->m_{n;n}\end{array}\right|$

La formula più semplice per calcolare il determinante è la formula di Leibeiniz:

Proprietà dei determinanti

• Il determinante è uguale a 0 se,
  • Due linee nella matrice sono uguali.
  • La matrice ha almeno una riga o colonna uguale a zero.
  • La matrice è unica.
• Sottraendo la riga i dalla riga j n volte non cambia il valore del determinante.
• Se due righe o colonne vengono scambiate, il segno del determinante cambia da positivo a negativo o da negativo a positivo.
• Il determinante della matrice identità è uguale a 1, $\det \left(I_n\right)=1$
• Le determinanti di A e la sua trasposizione sono uguali, $\det \left(A^T\right)=\det \left(A\right)$
• $\det \left(A^{-1}\right)=\frac{1}{\det \left(A\right)}={\left[\det \left(A\right)\right]}^{-1}$
• Se A e B hanno matrici della stessa dimensione, $\det \left(AB\right)=\det \left(A\right)\times \; <!--\; multiplication\; sign\; -->\det \left(B\right)$
• $\det \left(cA\right)=c^{n}x\det \left(A\right)$
• $\det \left(A\right)=a_n{a}_{22}\dots \; <!--\; horizontal\; ellipsis\; -->a_{nn}=\underset{i=1}{\overset{n}{\prod \; <!--\; n-ary\; product\; -->}}{a}_{ii}$ , se la matrice A è triangolare $a_{ij}=0$ et $i\ne \; <!--\; not\; equal\; to\; -->j$ , il determinante è uguale al prodotto della diagonale della matrice.

Metodo di calcolo determinante

Se A è una matrice nxn, la formula è:

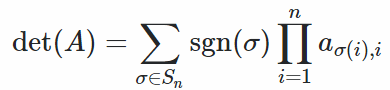
Esempio

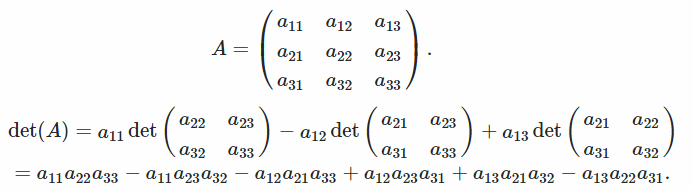
Questo metodo trasforma la matrice in una forma a scaglioni di righe ridotte scambiando righe o colonne, aggiungendo alla riga e moltiplicando un'altra riga per mostrare un massimo di zeri.

Per ogni pivot moltiplichiamo per -1.