Калькулятор определителя матрицы

Определитель квадратной матрицы $A=\left(a_{ij}\right)$ размерности n является действительным числом, которое линейно зависит от каждого вектора-столбца матрицы. Мы замечаем $\det \left(A\right)$ ou $\left|A\right|$ определитель квадратной матрицы A.

$\det \left(\begin{array}{c}{m}_{1;n}\dots \; <!--\; horizontal\; ellipsis\; -->m_{m_{i;n}}\\ ⋮\; <!--\; vertical\; ellipsis\; -->\ddots \; <!--\; down\; right\; diagonal\; ellipsis\; -->⋮\; <!--\; vertical\; ellipsis\; -->\\ m_{n;1}\dots \; <!--\; horizontal\; ellipsis\; -->m_{n;n}\end{array}\right)=\left|\begin{array}{c}{m}_{1;1}\dots \; <!--\; horizontal\; ellipsis\; -->m_{1;n}\\ ⋮\; <!--\; vertical\; ellipsis\; -->\ddots \; <!--\; down\; right\; diagonal\; ellipsis\; -->⋮\; <!--\; vertical\; ellipsis\; -->\\ m_{n;n}\dots \; <!--\; horizontal\; ellipsis\; -->m_{n;n}\end{array}\right|$

Простейшей формулой для вычисления определителя является формула Лейбейница:

Свойства определителей

• Определитель равен 0, если,
  • Две строки в матрице равны.
  • Матрица имеет по крайней мере одну строку или столбец, равный нулю.
  • Матрица уникальна.
• Вычитание строки i из строки j n раз не меняет значения определителя.
• Если две строки или столбца меняются местами, знак определителя меняется с положительного на отрицательный или с отрицательного на положительный.
• Определитель единичной матрицы равен 1, $\det \left(I_n\right)=1$
• Определители A и его транспонирования равны, $\det \left(A^T\right)=\det \left(A\right)$
• $\det \left(A^{-1}\right)=\frac{1}{\det \left(A\right)}={\left[\det \left(A\right)\right]}^{-1}$
• Если A и B имеют матрицы одинаковой размерности, $\det \left(AB\right)=\det \left(A\right)\times \; <!--\; multiplication\; sign\; -->\det \left(B\right)$
• $\det \left(cA\right)=c^{n}x\det \left(A\right)$
• $\det \left(A\right)=a_n{a}_{22}\dots \; <!--\; horizontal\; ellipsis\; -->a_{nn}=\underset{i=1}{\overset{n}{\prod \; <!--\; n-ary\; product\; -->}}{a}_{ii}$ , если матрица A треугольная $a_{ij}=0$ et $i\ne \; <!--\; not\; equal\; to\; -->j$ , определитель равен произведению диагонали матрицы.

Метод расчета детерминанта

Если A - матрица размера nxn, формула имеет следующий вид: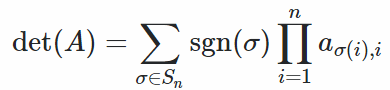

пример

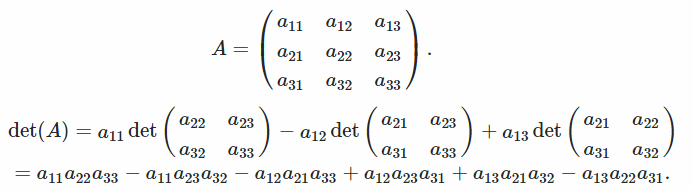
Этот метод преобразует матрицу в сокращенную форму эшелона строк, меняя местами строки или столбцы, добавляя к строке и умножая другую строку, чтобы показать максимум нулей.

Для каждого поворота мы умножаем на -1.