حساب محدد المصفوفة

محدد مصفوفة مربعة $A=\left(a_{ij}\right)$ من البعد n هو رقم حقيقي يعتمد خطيًا على كل متجه عمود في المصفوفة. نلاحظ $\det \left(A\right)$ ou $\left|A\right|$ محدد المصفوفة المربعة أ.

$\det \left(\begin{array}{c}{m}_{1;n}\dots \; <!--\; horizontal\; ellipsis\; -->m_{m_{i;n}}\\ ⋮\; <!--\; vertical\; ellipsis\; -->\ddots \; <!--\; down\; right\; diagonal\; ellipsis\; -->⋮\; <!--\; vertical\; ellipsis\; -->\\ m_{n;1}\dots \; <!--\; horizontal\; ellipsis\; -->m_{n;n}\end{array}\right)=\left|\begin{array}{c}{m}_{1;1}\dots \; <!--\; horizontal\; ellipsis\; -->m_{1;n}\\ ⋮\; <!--\; vertical\; ellipsis\; -->\ddots \; <!--\; down\; right\; diagonal\; ellipsis\; -->⋮\; <!--\; vertical\; ellipsis\; -->\\ m_{n;n}\dots \; <!--\; horizontal\; ellipsis\; -->m_{n;n}\end{array}\right|$

إن أبسط صيغة لحساب المحدد هي صيغة لايبينيز:

خصائص المحددات

• المحدد يساوي 0 إذا ،
  • سطرين في المصفوفة متساويان.
  • تحتوي المصفوفة على صف أو عمود واحد على الأقل يساوي صفرًا.
  • المصفوفة فريدة من نوعها.
• طرح الصف i من الصف j n مرة لا يغير قيمة المحدد.
• إذا تم تبديل صفين أو عمودين ، تتغير علامة المحدد من إيجابي إلى سلبي أو من سلبي إلى إيجابي.
• محدد مصفوفة الوحدة يساوي 1 ، $\det \left(I_n\right)=1$
• محددات A وتبديلها متساوية ، $\det \left(A^T\right)=\det \left(A\right)$
• $\det \left(A^{-1}\right)=\frac{1}{\det \left(A\right)}={\left[\det \left(A\right)\right]}^{-1}$
• إذا كان A و B لهما مصفوفات من نفس البعد ، $\det \left(AB\right)=\det \left(A\right)\times \; <!--\; multiplication\; sign\; -->\det \left(B\right)$
• $\det \left(cA\right)=c^{n}x\det \left(A\right)$
• $\det \left(A\right)=a_n{a}_{22}\dots \; <!--\; horizontal\; ellipsis\; -->a_{nn}=\underset{i=1}{\overset{n}{\prod \; <!--\; n-ary\; product\; -->}}{a}_{ii}$ ، إذا كانت المصفوفة A مثلثة $a_{ij}=0$ et $i\ne \; <!--\; not\; equal\; to\; -->j$ ، المحدد يساوي حاصل ضرب قطري المصفوفة.

طريقة الحساب المحدد

إذا كانت A مصفوفة nxn ، فإن الصيغة هي:

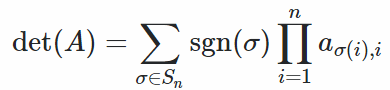
مثال

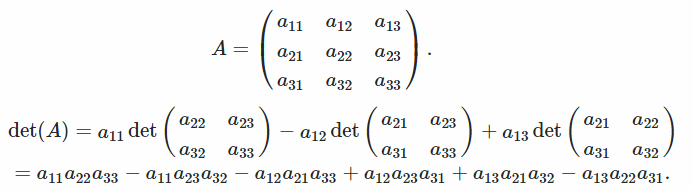
تقوم هذه الطريقة بتحويل المصفوفة إلى نموذج مرتبة صف مختزل عن طريق تبديل الصفوف أو الأعمدة ، والإضافة إلى الصف وضرب الصف الآخر لإظهار الحد الأقصى من الأصفار.

لكل محور نقوم بضربه في -1.