Calculadora de determinantes

El determinante de una matriz cuadrada $A=\left(a_{ij}\right)$ de dimensión n es un número real que depende linealmente de cada vector columna de la matriz. Apuntamos $\det \left(A\right)$ ou $\left|A\right|$ el determinante de la matriz cuadrada A.

$\det \left(\begin{array}{c}{m}_{1;n}\dots \; <!--\; horizontal\; ellipsis\; -->m_{m_{i;n}}\\ ⋮\; <!--\; vertical\; ellipsis\; -->\ddots \; <!--\; down\; right\; diagonal\; ellipsis\; -->⋮\; <!--\; vertical\; ellipsis\; -->\\ m_{n;1}\dots \; <!--\; horizontal\; ellipsis\; -->m_{n;n}\end{array}\right)=\left|\begin{array}{c}{m}_{1;1}\dots \; <!--\; horizontal\; ellipsis\; -->m_{1;n}\\ ⋮\; <!--\; vertical\; ellipsis\; -->\ddots \; <!--\; down\; right\; diagonal\; ellipsis\; -->⋮\; <!--\; vertical\; ellipsis\; -->\\ m_{n;n}\dots \; <!--\; horizontal\; ellipsis\; -->m_{n;n}\end{array}\right|$

La fórmula más simple para calcular el determinante es la fórmula de Leibeiniz:

Propiedades de los determinantes

• El determinante es igual a 0 si,
  • Dos líneas en la matriz son iguales.
  • La matriz tiene al menos una fila o columna igual a cero.
  • La matriz es única.
• Restar la fila i de la fila j n veces no cambia el valor del determinante.
• Si se intercambian dos filas o columnas, el signo del determinante cambia de positivo a negativo o de negativo a positivo.
• El determinante de la matriz identidad es igual a 1, $\det \left(I_n\right)=1$
• Los determinantes de A y su transpuesta son iguales, $\det \left(A^T\right)=\det \left(A\right)$
• $\det \left(A^{-1}\right)=\frac{1}{\det \left(A\right)}={\left[\det \left(A\right)\right]}^{-1}$
• Si A y B tienen matrices de la misma dimensión, $\det \left(AB\right)=\det \left(A\right)\times \; <!--\; multiplication\; sign\; -->\det \left(B\right)$
• $\det \left(cA\right)=c^{n}x\det \left(A\right)$
• $\det \left(A\right)=a_n{a}_{22}\dots \; <!--\; horizontal\; ellipsis\; -->a_{nn}=\underset{i=1}{\overset{n}{\prod \; <!--\; n-ary\; product\; -->}}{a}_{ii}$ , si la matriz A es triangular $a_{ij}=0$ et $i\ne \; <!--\; not\; equal\; to\; -->j$ , el determinante es igual al producto de la diagonal de la matriz.

Método de cálculo de determinantes

Si A es una matriz de n x n, la fórmula es: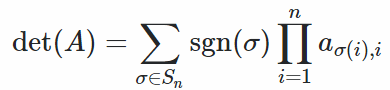

Ejemplo

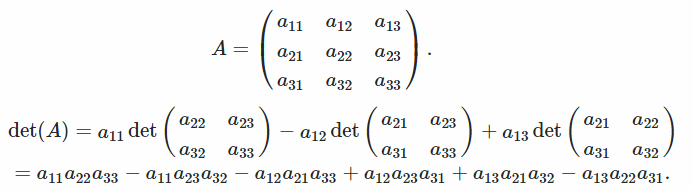
Este método transforma la matriz en una forma de escalón de fila reducida intercambiando filas o columnas, agregando una fila y multiplicando otra fila para mostrar tantos ceros como sea posible.

Para cada pivote, multiplicamos por -1.