Calculatrice de déterminant

Le déterminant d'une matrice carrée $A=\left(a_{ij}\right)$ de dimension n est un nombre réel qui dépend de façon linéaire de chaque vecteur colonne de la matrice. On note $\det \left(A\right)$ ou $\left|A\right|$ le déterminant de la matrice A carrée.

$\det \left(\begin{array}{c}{m}_{1;n}\dots \; <!--\; horizontal\; ellipsis\; -->m_{m_{i;n}}\\ ⋮\; <!--\; vertical\; ellipsis\; -->\ddots \; <!--\; down\; right\; diagonal\; ellipsis\; -->⋮\; <!--\; vertical\; ellipsis\; -->\\ m_{n;1}\dots \; <!--\; horizontal\; ellipsis\; -->m_{n;n}\end{array}\right)=\left|\begin{array}{c}{m}_{1;1}\dots \; <!--\; horizontal\; ellipsis\; -->m_{1;n}\\ ⋮\; <!--\; vertical\; ellipsis\; -->\ddots \; <!--\; down\; right\; diagonal\; ellipsis\; -->⋮\; <!--\; vertical\; ellipsis\; -->\\ m_{n;n}\dots \; <!--\; horizontal\; ellipsis\; -->m_{n;n}\end{array}\right|$

La formule la plus simple pour le calcul du déterminant est la formule de Leibeiniz:

Propriétés des déterminants

• Le déterminant est égale à 0 si,
  • Deux lignes dans la matrices sont égales.
  • La matrice a au moins une ligne ou colonne égale à zéro.
  • La matrice est singulière.
• Soustraire n fois la ligne i de la ligne j ne change pas la valeur du déterminant.
• Si deux lignes ou colonnes sont permutés, le signe du déterminant change du positive au négatif ou de négatif au positif.
• Le déterminant de la matrice identité est égale à 1, $\det \left(I_n\right)=1$
• Les déterminants de A et sa transposée sont égales, $\det \left(A^T\right)=\det \left(A\right)$
• $\det \left(A^{-1}\right)=\frac{1}{\det \left(A\right)}={\left[\det \left(A\right)\right]}^{-1}$
• Si A et B de matrices de la même dimension, $\det \left(AB\right)=\det \left(A\right)\times \; <!--\; multiplication\; sign\; -->\det \left(B\right)$
• $\det \left(cA\right)=c^{n}x\det \left(A\right)$
• $\det \left(A\right)=a_n{a}_{22}\dots \; <!--\; horizontal\; ellipsis\; -->a_{nn}=\underset{i=1}{\overset{n}{\prod \; <!--\; n-ary\; product\; -->}}{a}_{ii}$ , si la matrice A est triangulaire $a_{ij}=0$ et $i\ne \; <!--\; not\; equal\; to\; -->j$ , le déterminant est égale au produit de la diagonale de la matrice.

Méthode de calcul de déterminant

Si A est une matrice n x n, la formule est:

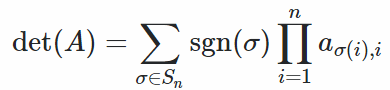
Exemple

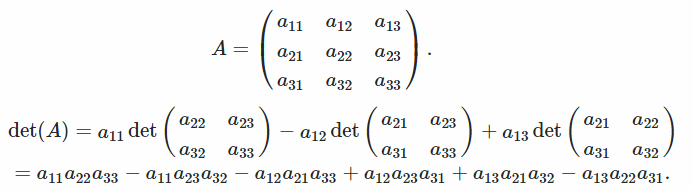
Cette méthode transforme la matrice en une forme d'échelon de ligne réduite en échangeant des lignes ou des colonnes, en ajoutant à une ligne et en multipliant une autre ligne afin d'afficher un maximum de zéros.

Pour chaque pivot, nous multiplions par -1.