calculadora de determinante

O determinante de uma matriz quadrada $A=\left(a_{ij}\right)$ de dimensão n é um número real que depende de forma linear de cada vetor coluna da matriz. Nós notamos $\det \left(A\right)$ ou $\left|A\right|$ o determinante da matriz quadrada A.

$\det \left(\begin{array}{c}{m}_{1;n}\dots \; <!--\; horizontal\; ellipsis\; -->m_{m_{i;n}}\\ ⋮\; <!--\; vertical\; ellipsis\; -->\ddots \; <!--\; down\; right\; diagonal\; ellipsis\; -->⋮\; <!--\; vertical\; ellipsis\; -->\\ m_{n;1}\dots \; <!--\; horizontal\; ellipsis\; -->m_{n;n}\end{array}\right)=\left|\begin{array}{c}{m}_{1;1}\dots \; <!--\; horizontal\; ellipsis\; -->m_{1;n}\\ ⋮\; <!--\; vertical\; ellipsis\; -->\ddots \; <!--\; down\; right\; diagonal\; ellipsis\; -->⋮\; <!--\; vertical\; ellipsis\; -->\\ m_{n;n}\dots \; <!--\; horizontal\; ellipsis\; -->m_{n;n}\end{array}\right|$

A fórmula mais simples para calcular o determinante é a fórmula de Leibeiniz:

Propriedades dos determinantes

• O determinante é igual a 0 se,
  • Duas linhas na matriz são iguais.
  • A matriz possui pelo menos uma linha ou coluna igual a zero.
  • La matrice est singulière.
• Subtrair a linha i da linha j n vezes não altera o valor do determinante.
• Se duas linhas ou colunas forem trocadas, o sinal do determinante muda de positivo para negativo ou de negativo para positivo.
• O determinante da matriz de identidade é igual a 1, $\det \left(I_n\right)=1$
• Os determinantes de A e sua transposta são iguais, $\det \left(A^T\right)=\det \left(A\right)$
• $\det \left(A^{-1}\right)=\frac{1}{\det \left(A\right)}={\left[\det \left(A\right)\right]}^{-1}$
• Se A e B têm matrizes da mesma dimensão, $\det \left(AB\right)=\det \left(A\right)\times \; <!--\; multiplication\; sign\; -->\det \left(B\right)$
• $\det \left(cA\right)=c^{n}x\det \left(A\right)$
• $\det \left(A\right)=a_n{a}_{22}\dots \; <!--\; horizontal\; ellipsis\; -->a_{nn}=\underset{i=1}{\overset{n}{\prod \; <!--\; n-ary\; product\; -->}}{a}_{ii}$ , se a matriz A é triangular $a_{ij}=0$ et $i\ne \; <!--\; not\; equal\; to\; -->j$ , o determinante é igual ao produto da diagonal da matriz.

Método de cálculo determinante

Se A é uma matriz nxn, a fórmula é:

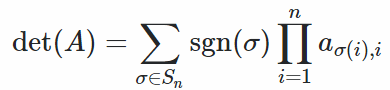
Exemplo

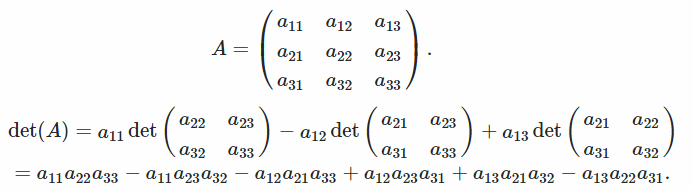
Este método transforma a matriz em uma forma escalonada de linha reduzida trocando linhas ou colunas, adiciona a linha e multiplica de outra linha para mostrar no máximo zeros.

Para cada pivô, multiplicamos por -1.